
Bouncing Barney
By Natalie Streiner
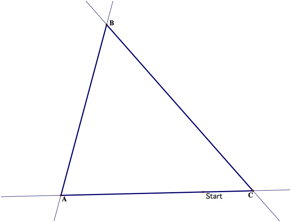
Barney is in the triangular room shown here. He walks from a
point on BC parallel to AC. When he reaches AB, he turns and walks parallel to
BC. When he reaches AC, he turns and walks parallel to AB.
First, Lets look at the path Barney will take when starting
at the chosen point.
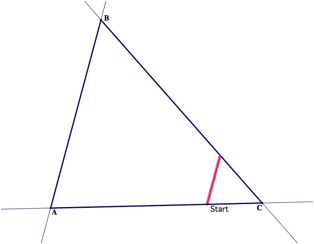

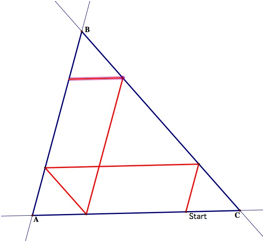
We see that Barney’s first step taken is parallel to
side AB. He walks until he reaches the wall. His second step is then parallel
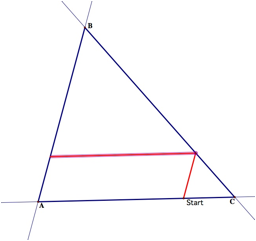
to side AC. From there he then walks downward toward side AC, taking a path
parallel to BC. He then walks upward once again taking a path parallel to AB.
His next step is parallel to AC again, and lastly walks his last step parallel
to BC. So, we see there is a pattern to his steps.
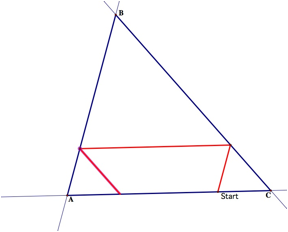
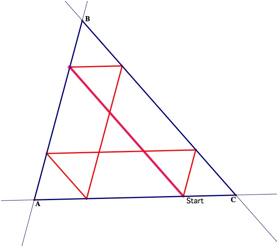
We also notice the triangles and parallelogram formed
by his path.
Here, we see the constructed congruent triangles and
parallelograms by Barney’s path.


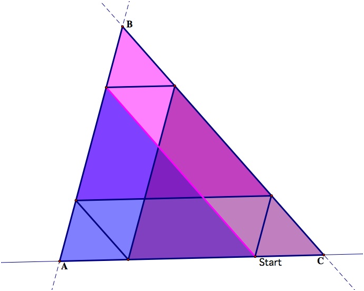
By the constructions of his paths we see that Barney
will always end up where he started. Turning (reaching the wall) five times
before returning to the starting point. This is assuming Barney starts at an
arbitrary point.
If Barney were to start at a vertex, he would simply
walk along the sides of the triangle, taking three steps and turning twice
before returning to his starting point.
If Barney were to start at the midpoint of a side, he
would walk the pattern hitting the midpoints of the other two sides. Therefore,
he would only take three steps and turn twice before returning to his starting
point.
So, we conclude Barney always returns to his starting
point.
Does Barney always travel the same distance?
Starting at an arbitrary point…
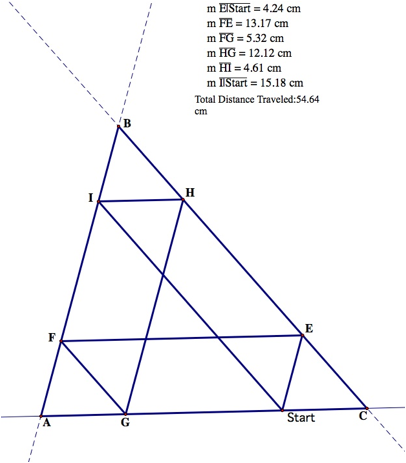
Barney travels 54.64 cm
Starting at a vertex…

Barney travels 54.64 cm
Starting at a midpoint…
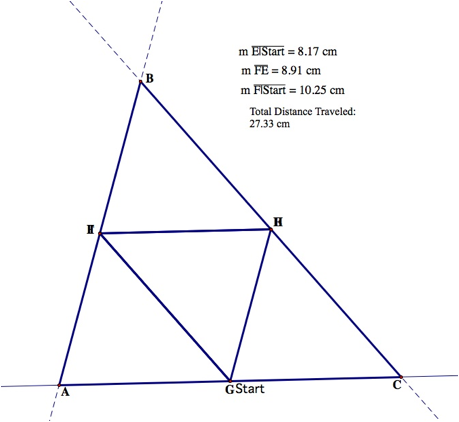
Barney travels 27.33cm
So, we see that Barney travels the same distance when
he starts at an arbitrary point or a vertex of the triangle. Barney travels a
much shorter distance when he starts at a vertex. We notice he travels exactly
half the distance when starting at a midpoint.
As mentioned earlier Barney’s path does construct
congruent triangles. They can be seen in the images
above.
We also have discussed that Barney travels half the
distance when starting at the midpoint rather than any other point on the
triangle.
What if Barney starts at the centroid?

Here we see if Barney followed the same pattern he
would take three steps and turn twice. We also see that if he starts at the
centroid he will be travelling the shortest distance, by far.
What if Barney started at the orthocenter?
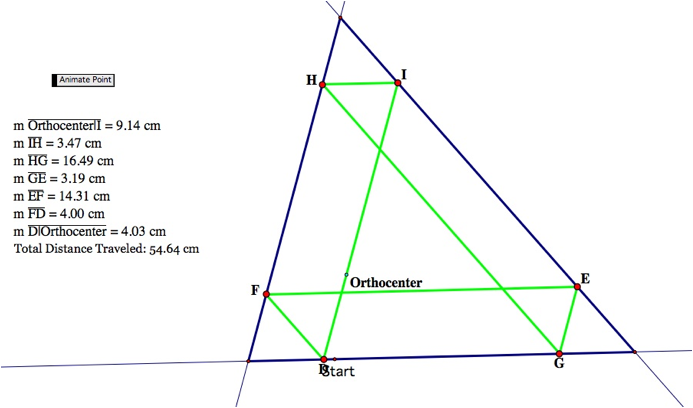
We see that this path is very similar to the path
Barney takes when he starts at any arbitrary point on the triangle. He takes
seven steps and turns six times when taking this path. We do notice that Barney
travels the same distance when taking this path as when he starts at an
arbitrary starting point.
In conclusion, we see that if Barney must start at a
point on the triangle he should choose the midpoint of the side. If he can
start within the triangle he should choose the centroid. This way, he will be
travelling the shortest distances, taking the least amount of steps, and
turning the fewest number of times.